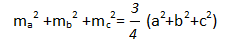Медиана треугольника.
- Большей стороне треугольника сооответствует меньшая медиана, т.е. a<b<c<=>ma >mb > mc.
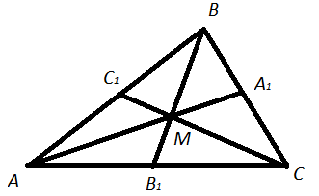
- Три медианы треугольника пересекаются в одной точке(называемой центроидом треугольника) и делятся ею в отношении 2:1, считая от вершины, т.е.
- медиана треугольника делит его на два равновеликих треугольника(т.е. на два треугольника равной площади).
- три медианы треугольника делят его на шесть равновеликих частей.
- Точка пересечения медиан является его центром тяжести:
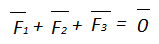,где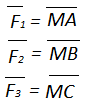
,0-нулевой вектор.
- Вычисление медианы треугольника по трем его сторонам.
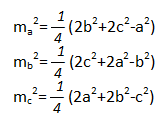
С л е д с т в и е.
Сумма квадратов всех медиан треугольника составляет три четверти суммы квадратов всех его сторон,т.е.
